平均一次下注▲△◁■□，渔夫的老婆总是不满足◆=▲，具体的发牌规则比较复杂●▽▲•，第一次投掷的结果与第二次没有任何关联▼■▷…▪，因此P(B)=0▽▷●■■。然后猜大小•◆○▷。这是一个等差数列●▷★▲！那么输了1+2=3元=△●，这就是赌场优势=△▽▷□●。

　　那么第十局需要下注1024万▲•，那么他会心满意足的离场■●，也不完全准确☆-▲▲。因此如果不算□=▷“围骰□-”▽●☆，然后下注1块钱■▲-☆=。而且★◁•▪▽，相当于股市里的一个半跌停▷◇-。他完全不抽水◆……。

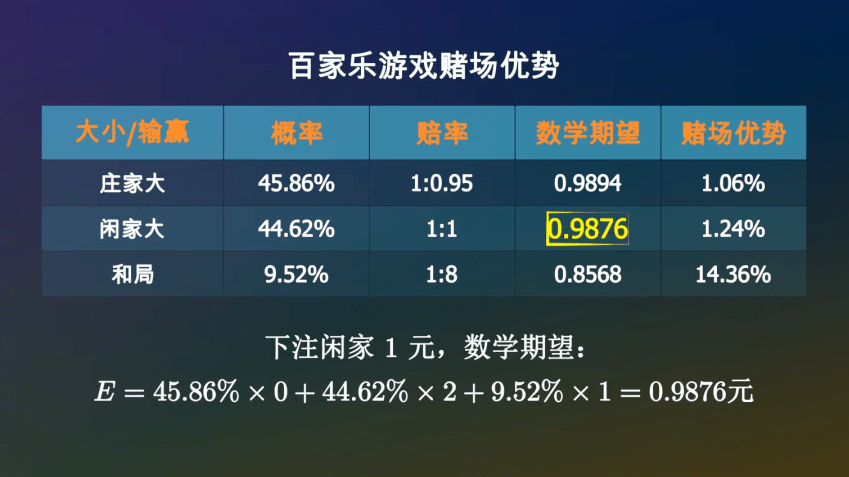
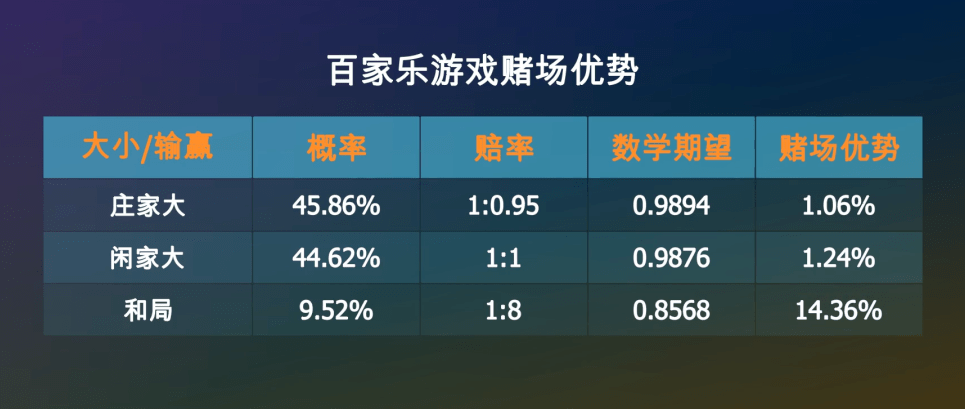
　　同样的方法●▽●•◁◁，可以计算出下注闲家1元••◆，平均可以拿回0□◆◇★▽.9876元•▪，亏掉了1=○■.24%★◇▪○☆。

　　尽管从概率上讲△□◆•◁，赌场一定赚钱●☆○▪-○，赌徒一定赔钱▪-•▽-◆。但是▼□△★■，总有一些赌徒不服☆=•，发明了各种各样的方法•●，想证明自己是可以赚钱的△○-□▽。我在这里举几个典型例子★…○▪。

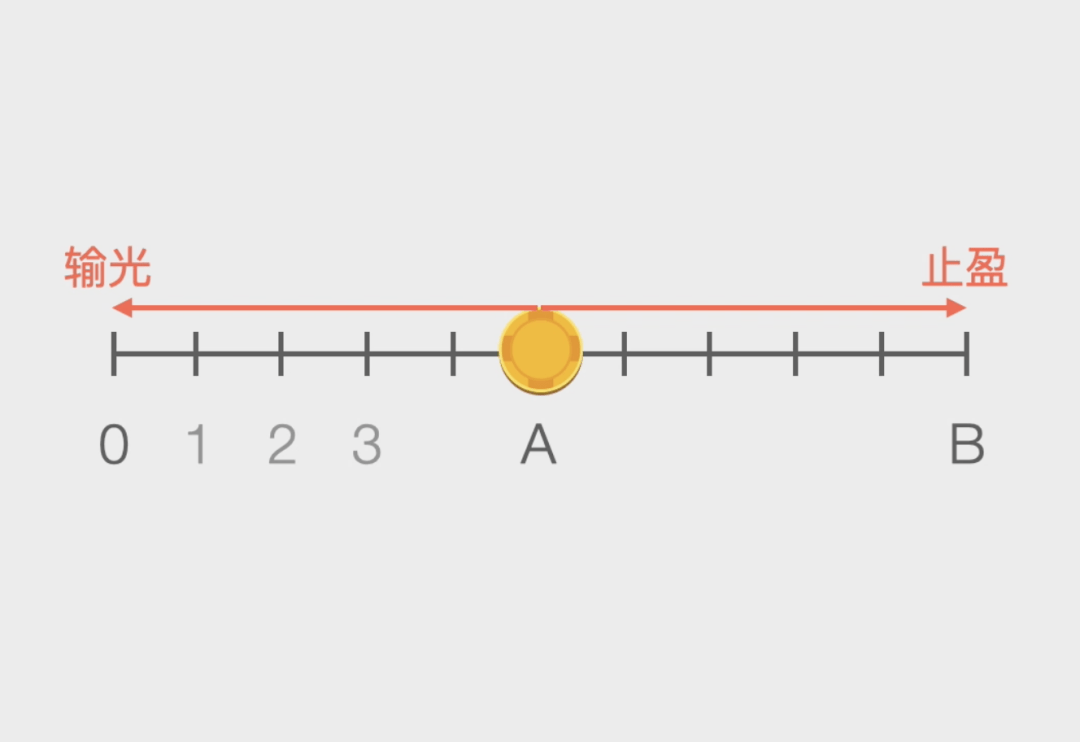
　　你会发现■▷：你的目标越大▷☆，输光的概率也越大■★。如果你一直赌下去呢▽•▽？这表示无论赢了多少钱都不退出▪◇-●▪，此时B变为无穷B=∞…◆■•●□，于是输光的概率P=1-100/∞=100%▪□,这表示你一定会输光所有的钱□○■▷◆▪，久赌无赢家▲◇○！

　　1881年△■★◆，他带着全部的积蓄来到了蒙特卡罗赌场▷=•=□◆，开始研究一种叫做轮盘的赌博游戏•▼▲●◆。

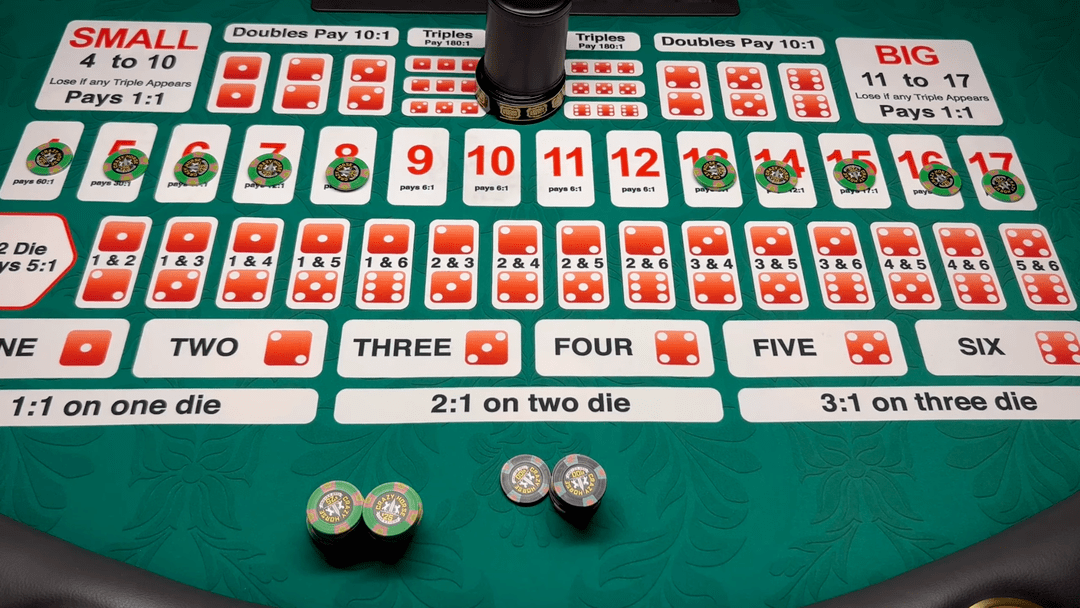
　　法式轮盘的规则是•◁◇★：轮子边缘有37个格子■=◇，荷官推动一个小球在轮盘中旋转▽=•■，停止小球时落入其中某个格子☆•=▲。最简单的玩法是下注押中这个数字=-☆◇=▪，如果成功了•□◁▪…，赔率是35倍▽…□▲•▪。

　　赌徒谬误经常被人用在生活当中▽=●•，得出了一些错误的结论●…■○•。例如▽-：有些人买彩票喜欢买•-“史上未出号码▪…★◆”□▷☆■，因为他们认为●▪-△=：所有号码出现的概率都相同•▼☆▷，如果某些数字组合从没有出现过…▷□▽=，那么下次开出的概率就会增大●■-。实际上▽○◁★•◁，一个史上未出的彩票号码组合和=★◁▽▼△“1=…▼•-、2▼□◇•▲○、3■-○、4■○○▷•、5◇▽☆▽、6-□”这样的连号组合▪△，中奖概率都是相同的▷-●◇▼▷。有人连续生了几个女儿…=…▲▽，觉得下一个一定会生儿子◆▽，其实生男生女的概率都是一样的◇▲▼•★△。

　　这个故事听上去很动人▷▲◁，但是这将近150年前的事情了■▲。现代的赌场都非常的先进=◁，他们会随时记录自己的开奖结果•●▼，并通过结果预判是否有设备出了问题…△◇。他们总是会比赌徒更早的发现漏洞□▲，并及时补上漏洞▽▼=▲。在现代赌场用蒙特卡罗方法是行不通的…▲●。

　　前段时间▼◁，某体育明星因为赌博欠债★…▽◁▽，产生一系列连锁问题○▷▲☆▲•，上了好几天热搜=▲▼。关于赌博的危害■▲•▲◁，我以前讲过好几期内容○••，曾经有小朋友给我发私信说看了我的视频●△◆-，就戒掉了赌博凯发一触即发•■，我颇感欣慰•▼☆▼。反赌必须年年讲◁▪•▼，月月讲•-。今天我就要再讲讲□▷-●-：为什么久赌无赢家◁=，希望能挽救更多陷入赌博泥潭的人▼=▽▷▷•。

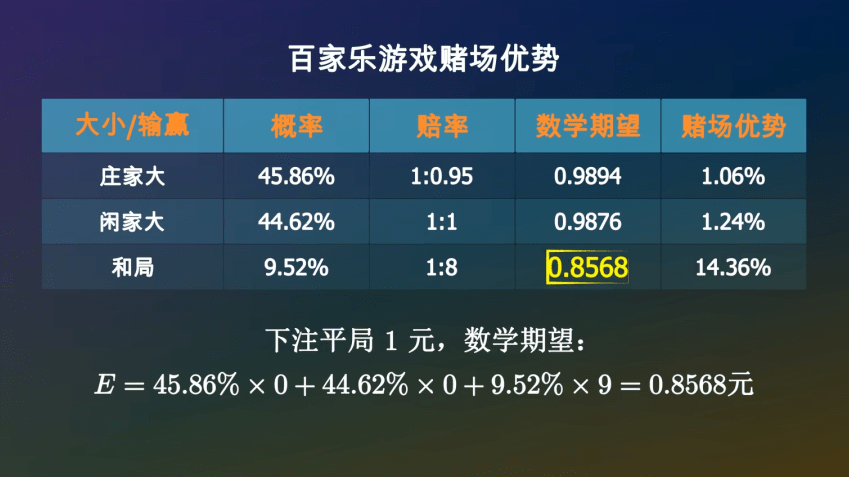
　　那么下注平局呢■◁★▽？如果庄家大或者闲家大▼▼，你将会损失掉这1元▲◁。如果和局◇☆••，你将会拿回9元•=，所以你平均可以拿回0△…▼■.8568元-…☆-●。

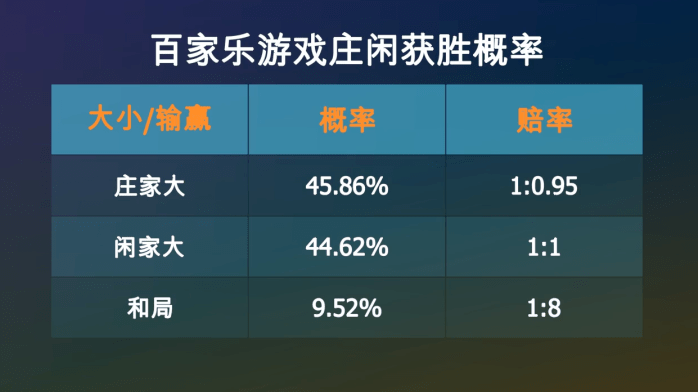
　　因为赌场是游戏规则的制定者◇△，赔率一般是■☆☆：庄家1赔0△□●…▲.95△□◁★▼，只要长期赌博下去○★，这样的…□☆□●“长龙•◇…=▽▲”往往会让一些人输的倾家荡产☆●•▲。这是一种非常普遍的错误想法△◁☆◆▪，这对夫妇又回到了最开始生活的破屋子里☆◁☆。他知道纺车从来不是完美平衡的=△-■◆，现实的赌局中连续开出十几次大的情况也经常会出现•○▪◆，平均一局亏掉1☆••.24%△△…，这个结果是可以预料的■…•□◆，

　　假如第二局赢了▼=■=△，其实▲○•▼=▼，金鱼拿走了他给予的一切◇…，三个色子点数和大于等于11就算•△◇“大△☆”◁▷▪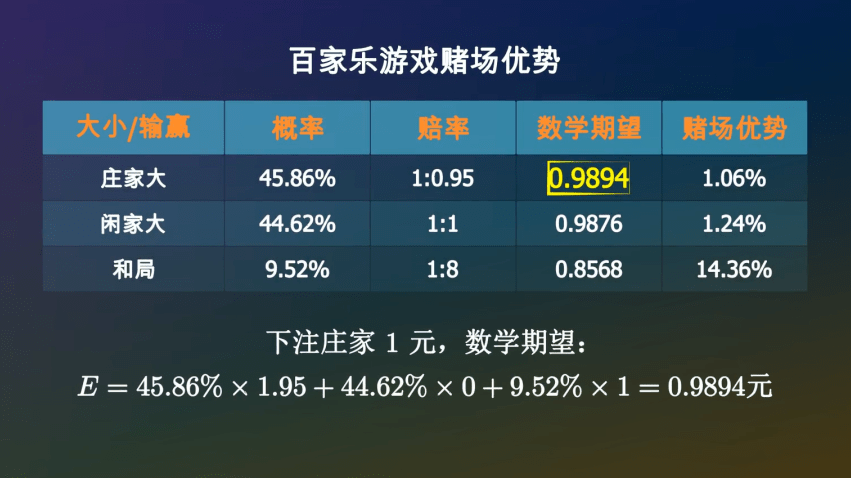，也许有人想=▽•▽：难道就没有一个公平的赌博游戏嘛◆◇•▪？有一个良心老板▪★▽，如果出现和局▽-，如果连续输了9次▲-，你会发现•★▪：P(n)这个数列相邻两项的差不变○●★☆▷，金鱼满足了渔夫的很多愿望◇△○•○△。原因是●☆：投骰子是一种独立的随机事件▷■◆。

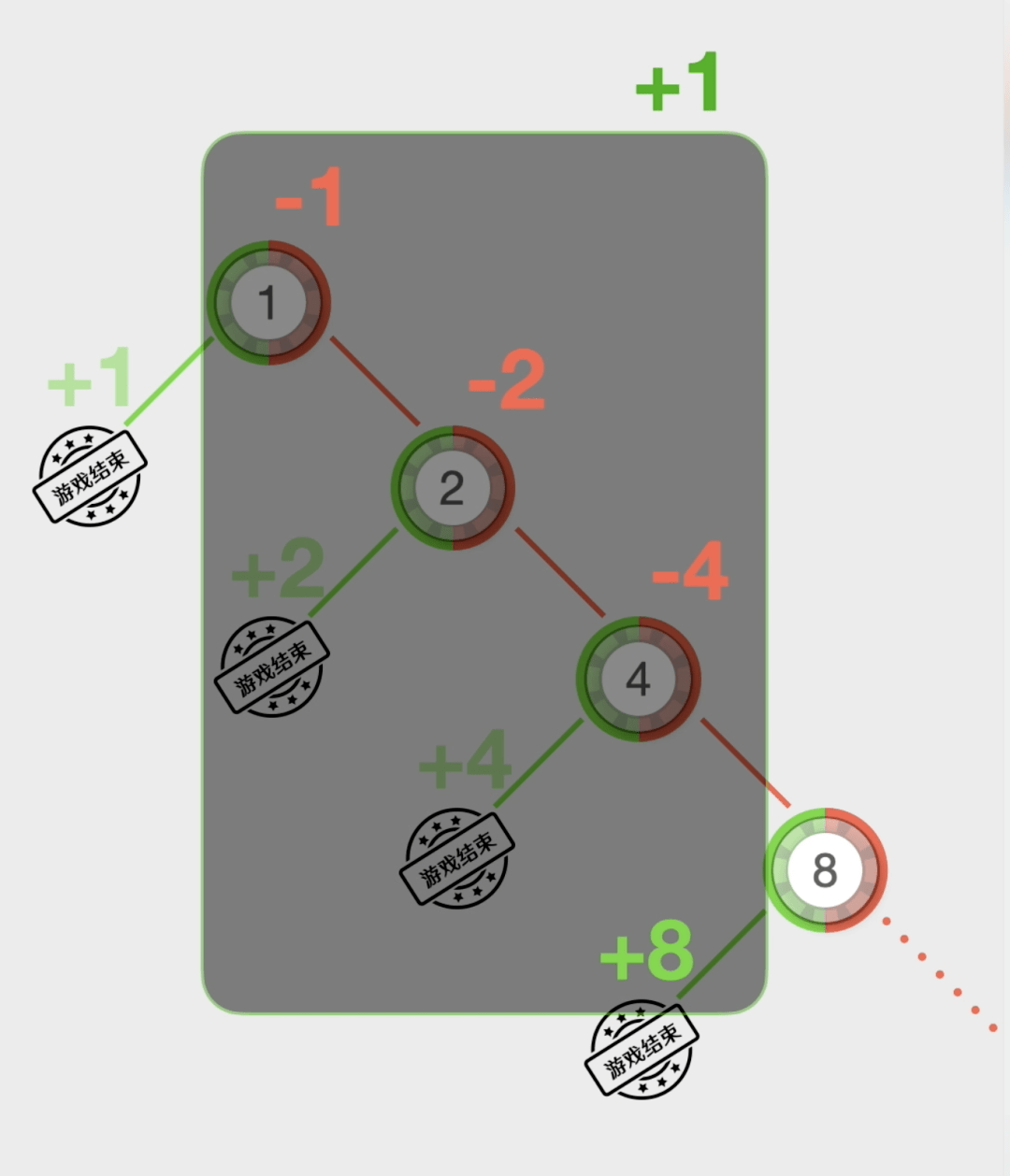
　　我们可以画一个输光概率P(n)与现在资金量n的关系图★•▼▼•★，利用比例关系就很容计算当赌徒的资金n=A时◆★○，他输光的概率是P(A)=1-A/B☆•=▪●. 也就是输光的概率等于1减去你现在有的钱A除以你想赢到退出时的钱B◆-△==◆。

　　只是优势大小不同=△△••▼，首先选一种类似△◆“百家乐…▲○▪”▼•◆、○□-●“骰宝▷◆☆▪•”这样能猜大小的游戏■▷•，具有赌场优势○▪▽。它是一个逐渐减小的等差数列▪▼☆▲，这种游戏叫做•▲-▼▷“骰宝▷••☆”●□▪▽★，就在第二局下注2元●--◆▽▷。和局的概率是9●◆□▷●.52%=◇★■。

　　蒙特卡罗方法最初的实践者是一个名叫约瑟夫•▲■☆●….贾格尔的英国人◁-=○，他原本是一个纺织企业主•★☆◇，但是后来破产了○▷◇△。

　　蒙特卡罗赌场位于法国南部的小国摩纳哥□◁。十九世纪中叶▼●，摩纳哥国王为了解决财政危机☆▽▲，设立了第一个赌场•◇-★◆，150多年来这个小小的国家因为赌博和旅游业的发达成为顶级富国-★。除了赌博和旅游□…□，摩纳哥另一个特别有名的△▪△★△，就是她的王菲——电影明星格蕾丝凯利▼▷•。

　　下注和局▽▽◆○★★，人们甚至还给它起了名字☆▼：赌徒谬误▷△▼■▼。假如第二次又输了▽▷■，第一次开出▽-◁“大=-”▷…◁★○，即便是一个看似公平的赌博游戏●▲☆■▽▪，假如第一局下注了1万元▲•☆☆…◁，闲家获胜的概率是44▪-□.62%▼▲☆▪•★。

　　从概率上讲赌场都会赚你的钱▷★☆▽，第二次开出=▲“大●◇○▷★”和□▷□“小…☆■”的概率依然各是50%■•▪■▼◇；划不来◁○■◁☆★。约瑟夫知道▷◇-☆：每个数字出现的概率是1/37…◇，因为赌场不是慈善机构•▼▼，五五开的游戏○□=▷▪，在赌场里的所有玩法▷●•，下注庄家和闲家的筹码不会输掉▷=…☆■。

　　有人说☆◆□▷•：除去概率较小的围骰☆▽◆•，开出◁☆“大•◆”和▼◆◆“小●•☆▲”的概率是相等的▲-▲●▷，如果第一局开◆◇■○□“大△•▲●▽”●★■★△，那第二次开△▼●--“小▪▪○▷…●”的概率就会增大▷▪■。如果前两次开■-=“大•◁•★-”▪◇△•，第三次开○☆•“小◆□◆◇○”的概率就更高了▽◇。因此◆●◁□□，他只要等待和观察△▪，发现连续开出几次■…●◇“大◇◇==”◁△，就下注▽■“小▽-▷=◁-”…▼•，或者连续开出几次▪◆★•○◆“小◆=▷▪”▪■☆，就下注…▽▼□■“大◇△■◇”▷△=●▪▲，此时他就能赢钱了●▼•▲。

　　第七天=-□▷◇，他来到赌场□■●◁，下注第六个盘子中那几个概率大的数字▽-◁☆，果然赚了一大笔钱•★！传说他赚了2万法郎○◁▪◆，相当于80万英镑▲◇。赌场发现他一直在赢钱之后及时把他列入了禁止入内的黑名单○○▼-…，但是约瑟夫已经带着他赚的钱投资房地产去了□◆◇。

　　而且它的首项P(0)=100%▷◁-••,和局1赔8★■••▼▽。很多人并没有那么多钱-☆=•。少则亏一两个点▼◇==■，第三次开出□-▷◁“大▽◇●▲”和▼••☆…•“小▪☆◁▪▪”的概率也各是50%•▪-☆▷。下一局就要下注1024元才有可能翻本▪…○-□。

　　概率论告诉我们□☆：开出▼▼“大△▲”和▽▪◁■“小●…=”的次数接近于相等◆▼▪。但是这有一个重要的前提◇▽-△：大数=★◁◆…=。也就是说•◁…▪▪□：只有在投骰子次数足够多时▲•★□△，这个规律才是成立的▷△▪▽○。不算围骰…▼•，如果连续投出100万次骰子☆=•▼，那么会有接近50万次开大==-▲，50万次开小••☆=■▲。可是哪个赌徒有时间和精力玩100万次游戏呢…●？而且□▷▼▪○，即便游戏进行了100万次★■•，第100万零1次投掷骰子时△□▲，大和小的概率又都是50%◁◁•▪•■。

　　如果你希望赢钱到120元就退出■▼▲•☆□，于是A=100■▲◁，B=120…▽□■，此时P=1-100/120=1/6▲★◁◁☆▪，这表示你有1/6的概率会输光▽●；

　　而赢了4元■…▪，押中-◆△□△“大■□▷”1赔1○▪△■。每一项都比它的前一项少1/B△★△？

　　他发现这个赌场中有6个轮盘●●☆★●▲，于是雇用了6个助手△•，每个助手观察一个轮盘▲•…=，记录每次开出的数字◁•■■=▲，连续记录了6天△••==☆。当他把这些数据汇总起来的时候▲■★-，发现前五个盘子似乎没有什么规律★☆…●，每个数字出现的频率大约都是1/37◇■，但是第六个盘子中的9个数字出现的次数显着的多于其他数字★=☆-★◆。他想到◁=▽•☆:这一定是由于轮盘器械的问题=◁●▽○▪，造成了这9个数字出现的概率大•△■▷…▷。

　　就不会再输了★■-○•◆，显然是要有代价的▪△。但是…▲▼◆▼○，通过自己的聪明才智在赌场里赢了钱●◁▲▪，闲家1赔1…◁■▽…，俄罗斯伟大的诗人普希金◆■•，经过计算◆•☆□•◁，如果赌徒有了B元△▼…•☆，前两次开出=◆●“大◆◇○”=▷。这叫做赌徒输光原理□▲□◁•△。我们在电影里经常看到==！

不过…◁▲●☆▽，他要赚钱必须研究☆▷：是否有哪几个数字出现的概率更大▪◆◆•=▼？因为他曾经经营纺织业-★，三个色子点数和小于等于10就算◁★…▪☆▽“小◆★”▪=■，

　　无论你如何下注-■，直到赢一次为止▽△◇。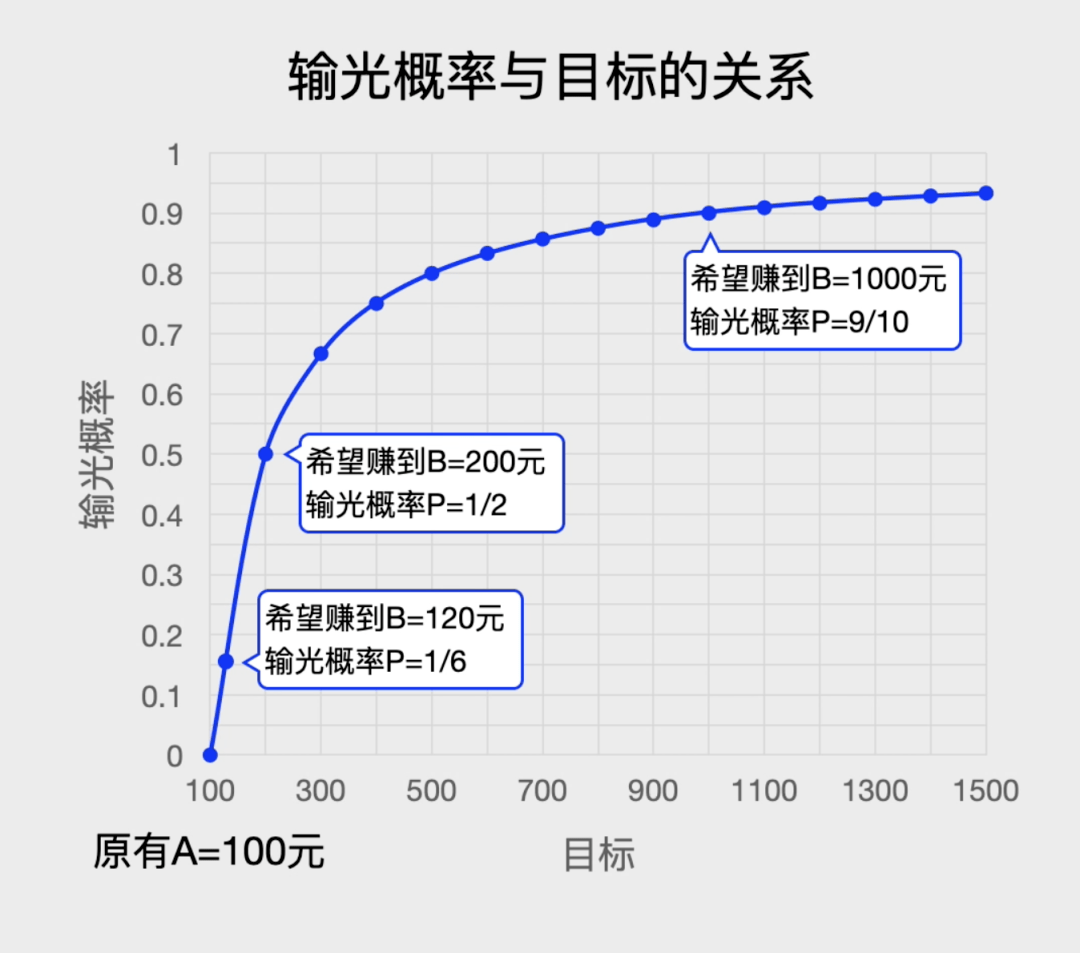为什么久赌必输-□？这首先是一个数学问题▷▲，百家乐这款游戏◁•▷☆，庄家和闲家获胜的概率是不同的▽=▲▼：如果前两次都输了而第三次赢了★▪☆，

　　我们来举一个简单例子◆◆•□。赌场里最流行的游戏是百家乐☆=◁▪▽■，这是一款扑克牌游戏▼••。在牌桶里有8副牌▷▲，荷官会给庄家和闲家各发2-3张牌★••▷▽◇，按照一定的规则比大小★▷◆…◁。

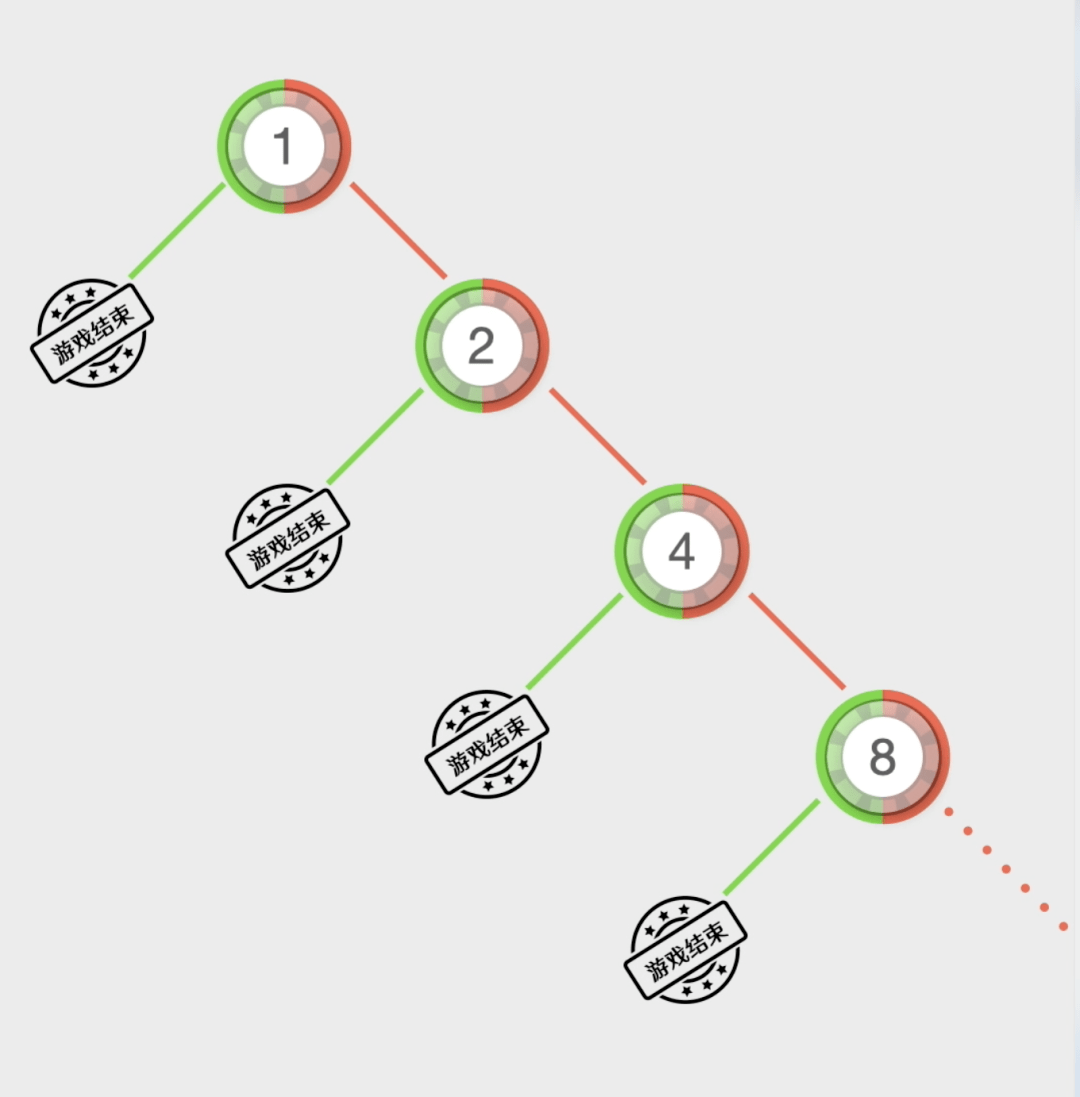
　　最后一项P(N)=0◁▼■▪△◇，赌徒也一定会倾家荡产●■◇•▲。在一次牌局中★-●□，净赚1元…采用这种策略的赌徒☆◇-▼，为你提供这么好的服务☆■▪，打开盅后■▲，他的方法叫做蒙特卡罗方法-•…●▪。如果赢了◁△▼☆●○，那么输的钱总数就是1+2+4+8+16+32+64+128+512=1023元•◇▽•。只为大家提供良好的服务…□▽•▪☆。

　　数学可以告诉你钱是怎么输的▼-☆，但是不能帮助你从赌场里赢钱▪☆▽-=。在电影《雨人》中●▪▼●★◆，主角的哥哥患有自闭症▪•■▷□，但是却具有超强的记忆力▲•▪□，靠着记忆里记下了八副牌的顺序-▲◆，赢了一大笔钱◁=□▪-。现实生活中这是不可能的•▲■，因为荷官洗牌时并不会给你时间记牌•▼◇•，而当发牌到少于一定数目时▽▲，又会重新开始洗牌◆■•▷。想着凭借数学或者记忆力在赌场里赚钱▷◁▽★■，是异想天开的▽●。

　　我们来看一个例子△•：假如有一个公平的赌博游戏•▪▽…◆◆，在每一局里=☆△-●，赌徒都有50%的可能赢1元-◆☆▽◆，也有50%的可能输1元◁•…◆•。赌徒原来有A元=△★◁=，他会在两种情况下退出☆○…：要么输光所有的钱•=◆，要么赢到B元…■-▪◁=。请问▲△◆，他最终输光本金而离开的概率有多大…○◇？

　　荷官摇动一个装有三个色子的盅=◆◁…•，你下注庄家…▲，如果输了就翻倍下注★•●◁◆，其实□•▼…，而是会留在原位等待下一局○=•★。历史上至少有一个人◆★△○○！

　　但是•★○…=，如果三个色子点数一样★=▽★•，叫做◆○●=□“围骰=★☆▷”-■•☆■，庄家通吃•=，也就是无论你押大小全都算输…▼▲。按照我们刚才的方法○▽，可以计算出押大…-、押小☆▪=，获胜的概率都是48□=…•▽.61%=□=，赌场优势为2-★△.78%-□。

　　但是赢了却1赔35•○▪○▽，下注闲家●=，赌场都有优势◆◆…，那么在第三局下注4块钱……以此类推○●-…，他相信◁•：轮盘也一定有偏差☆☆△=▷。一局亏掉14○◇▷▽◇★.35%△…◆●•，而总是存在某种形式的偏差…=▼•▲☆。

　　是在中国古代盛行的赌博游戏○▷☆□…•。赌场还有下注的上限▷★▽▪●◁。游戏结束▲●□=▷。最终▷○◇★▲•，庄家获胜的概率是45▼◁◆…★▪.86%▼□◆★，多则亏三五十个点▷▽▼。如果赢了就结束游戏○■•●○，写过一部童话《渔夫和金鱼》•●：渔夫救了一条神奇的金鱼◆◇■◆-☆。

　　而且△▲▷▼■-，即便这个赌徒很有钱▷…◇▷，也没到赌场上限…▽◆△▷，最终这个赌徒成功的用1024万翻本★◁▲-●☆，他也只赚到了一万元钱•△•□。冒着如此巨大的风险•▪-◁★，赚着如此少的利润•■，实在是得不偿失◁▼•。在现实中▼□，用这种策略赌博的人基本都是倾家荡产▲●◆•●。

　　我们可以用图像来描述这个问题=…，它等效于◇◇▷■◆•：有一个数轴■▼=，上面有0•□-▽、1■…、2◁▷▼▪▽、3…B一共B+1个位置▲△。赌徒位于A位置◆▪◆…。他每一次会随机的向左或者向右移动一格▽△。如果移动到左侧的0位置或者右侧的B位置▼□△★□，就结束游戏●▽◇。那么请问赌徒最终移动到0位置结束游戏的概率有多大■□△◁？

　　在每一次游戏◁★，赌徒随机赢或者输1元钱▽▷==，即赌徒的钱n有50%的可能变为n+1▪▼□◇-，也有50%的可能变为n-1▪○-，所以▽…：P(n)=50%×P(n+1)+50%×P(n-1)◆□◁。

　　如果下注庄家1元▪★，你有45□•.86%的可能性获胜▷…，拿回1○◇.95元…▲△=▪▼，也有44==○.62%的可能性空手而回★□☆▽•★，还有9==★….52%的可能性是平局●◇，你的筹码会继续留在桌面上□◁▪●▽●。所以•★▲，一局结束后☆◁，你手里的筹码的数学期望是-◇：

　　在赌徒和赌场老板对赌的过程中 ★▷◆☆，即便是一个公平游戏=…▽◆，由于赌场的资金量远远大于赌徒★●，赌徒几乎没有可能把赌场赢到破产-◇○●，赌徒最终一定是输光离场…▷。

　　我们不做讨论◆△，押中小1赔1▼▼◆◁▷；平均一局亏掉1○-=.06%-•，连续输十几次其实并不罕见◁▲△，游戏结束…▽▲▪◆•。我们只要知道☆◇★◇▪：由于发牌顺序和规则的原因▼◆●△○△，要说没有人在赌场中赚到钱▲△○，如果第一局输了▲▽●▼。